Conhecer sua ferramenta de trabalho pode não ser o suficiente para desenvolver um projeto de design consistente. Design vai muito além da ferramenta usada ou mesmo de conhecimento em geometria, mas isso não significa que um ou outro não tenham importância durante um processo criativo.

Objetivo desse vídeo é te mostrar diferentes maneiras de pensar e construir formas geométricas do nosso cotidiano. Você verá, entre outras coisas, como construir um retângulo áureo, um pentágono e que relações um tem com o outro.

Espero que este vídeo ajude você a buscar novos conhecimentos e se inspirar cada vez mais.

Referências citadas

Livro

Geometria do design – Kimberly Elam

Pessoas citadas

Jan Tschichold
Gustav Fechner

Cliente demonstrado no vídeo

Aires - soluções ambientais

CRÉDITO

Projeto Festa das Nações
Mundo Studio

Abaixo segue a transcrição do vídeo.

Introdução

E aí galera, beleza?

Walter Mattos novamente, e antes que você pense que eu quero te convencer de que geometria não é importante só porque você já conhece o Illustrator, ou qualquer outro programa gráfico, saiba que o intuito desse vídeo é estimular justamente o contrário, ou pelo menos te dar um novo ponto de vista.

A verdade é que por mais que você domine uma ferramenta, o conhecimento isolado dessa ferramenta não te faz especialista em nada a não ser na própria ferramenta. Caso contrário seria o mesmo que dizer que já que eu sei bater um martelo e apertar um parafuso, eu sou um marceneiro e posso construir uma cadeira se eu quiser.

Para você se especializar em qualquer profissão é importante que você estude bastante, claro, e no nosso caso não é diferente. Design é linguagem, metodologia, semiótica e entre milhões de outras coisas é também geometria e, claro, conhecimento da ferramenta de trabalho.

O problema é que às vezes por nos habituarmos ao uso da ferramenta a gente acaba esquecendo alguns princípios e metodologias básicas que muitas vezes podem nos ajudar em um processo criativo.

E uma prova disso é que eu mesmo, quando falei sobre a construção do cartaz Konstruktivisten, disse que não sabia por que o Jan Tschichold tinha inscrito um pentágono dentro de um círculo.

E como alguns leitores me lembraram, na verdade ele fez isso porque como na época o processo de construção era manual, ele precisava do círculo para construir o pentágono. E isso é uma coisa relativamente óbvia, mas eu acabei esquecendo por conta das facilidades que o Illustrator me oferece.

Por isso eu decidi gravar esse vídeo. Primeiro para você não cometer o mesmo erro que eu, e também para te mostrar que é possível equilibrar as duas coisas, o conhecimento do software com um pouquinho de metodologia ou mesmo um conhecimento básico em geometria.

Então para estimular o exercício criativo eu vou começar te dando um exemplo de construção geométrica de uma forma que você, designer, utiliza com bastante frequência e talvez não saiba. Essa forma é o retângulo raiz de 2.

Retângulo raiz de 2

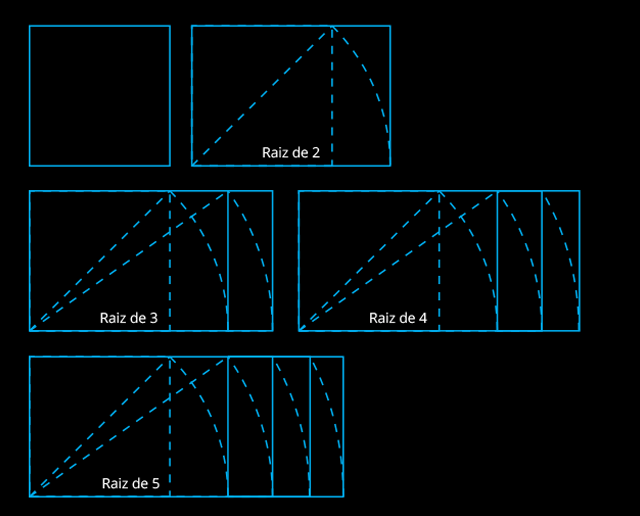
Criar um retângulo raiz de 2 é bem simples, e você já vai entender porque ele recebe esse nome.

Eu começo com um quadrado, traço uma linha diagonal nele e giro essa nova linha até ela encostar na base.

Agora é só aumentar o quadrado até a largura da linha e pronto, você tem o retângulo raiz de 2.

E por que esse retângulo recebe o nome de “raiz de 2”?

Primeiro deixa eu ver qual é a raiz de 2, né? Vou abrir a calculadora, digitar 2 e clicar no botão “raiz quadrada”. O resultado é 1,414 e alguns quebrados.

Então, voltando para o retângulo, se eu pegar a largura dele, 212,133 e dividir pela altura, 150, eu tenho o valor 1,414. Ou seja, a relação entre os lados desse retângulo sempre vai resultar em 1,414, que por acaso é a raiz quadrada de 2, e por isso ele recebe esse nome.

Viu? Molezinha.

Mas eu falei que você, designer, talvez utilize esse formato sem saber. Então para te dar um exemplo bem simples e que com certeza faz parte do seu cotidiano, vamos usar o papel A4, como exemplo.

O A4, como você deve saber, possui 29,7 por 21 centímetros.

Se eu pegar 29,7 e dividir por 21, o resultado é 1,414.

Ou seja, nem mesmo o formato do papel que você utiliza para imprimir o seu layout foi criado de forma aleatória. Ele tem um porquê de ser do jeito que você conhece.

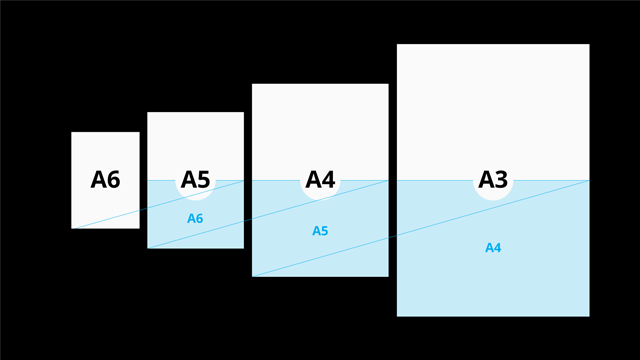
O mesmo vale para os tamanhos A3, A5 ou qualquer outro papel dessa série A, já que um é sempre o dobro ou metade do outro, como você pode ver na imagem.

E partindo do retângulo raiz de 2 eu também consigo encontrar uma outra forma geométrica bem interessante, que é o retângulo raiz de 3. Pois é.

Retângulo raiz de 3

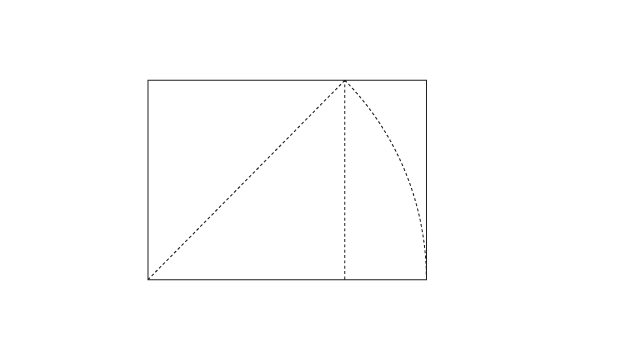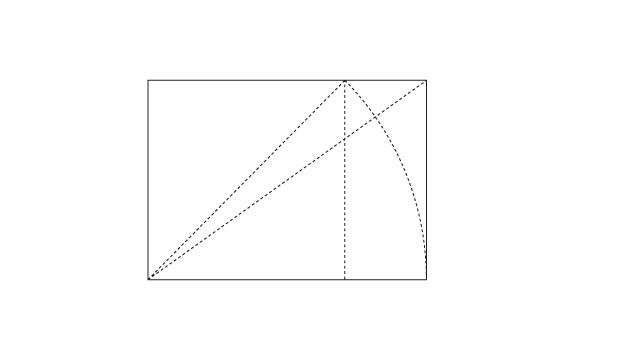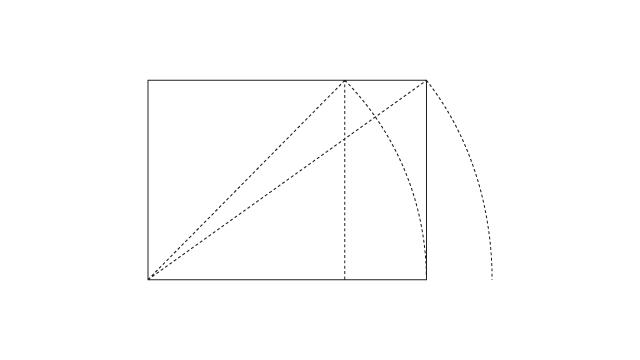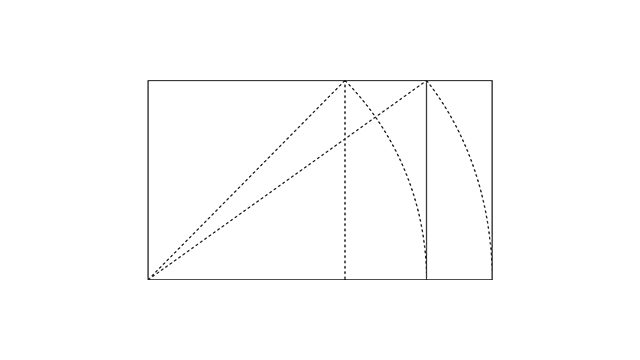
O procedimento de criação do raiz de 3 é exatamente o mesmo que o anterior, só que dessa vez ao invés de partir do quadrado, a gente começa pelo próprio raiz de 2.

Traço a linha diagonal, giro a linha até ela encostar na base e aumento a largura do retângulo até encostar na linha.

E como você já deve desconfiar, a razão pela qual ele recebe esse nome é a mesma também.

Se eu procurar a raiz de 3 encontro o valor 1,732, e se eu dividir a largura do meu retângulo, 259,808 pela altura, 150, meu valor é 1,732.

Mas e se eu quiser encontrar ele partindo do quadrado aqui no Illustrator, é possível?

Claro que sim.

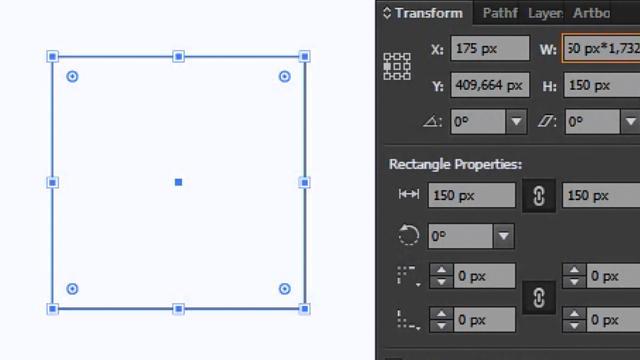
Primeiro eu vou criar um quadrado com a mesma altura do nosso retângulo e arrastar ele pra baixo.

Seleciono ele, vou na aba “Transform”, marco o eixo central esquerdo como ponto de referência para o meu ajuste, desabilito a função de manter as proporções, clico aqui ao lado do valor da largura e simplesmente multiplico esse valor por 1,732 e aperto “Enter”.

Pronto, a gente recriou o retângulo raiz de 3 em segundos, sem precisar passar pela etapa de construção.

E o que é melhor, agora a gente conhece duas formas diferentes de construir o mesmo objeto.

O raiz de 3 ainda possui uma curiosidade. Se você dividir ele em 3 partes, estes 3 retângulos também são retângulos raiz de 3.

Hexágono

E partindo do retângulo raiz de 3 a gente consegue construir um novo objeto, e esse novo objeto é o hexágono.

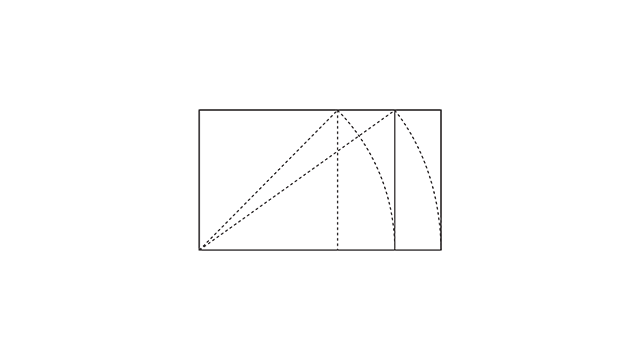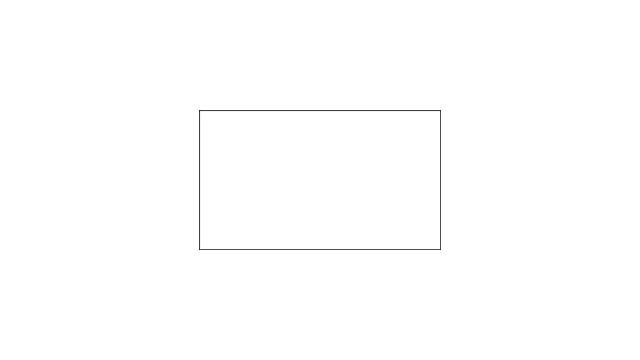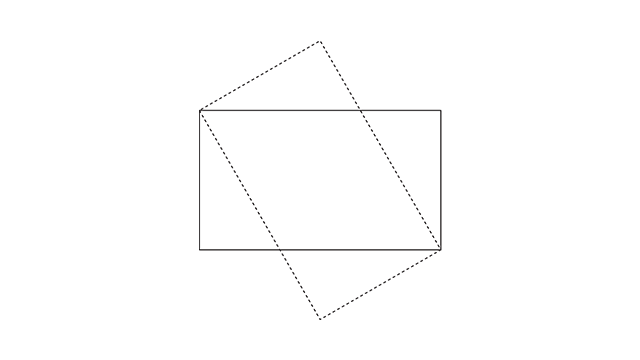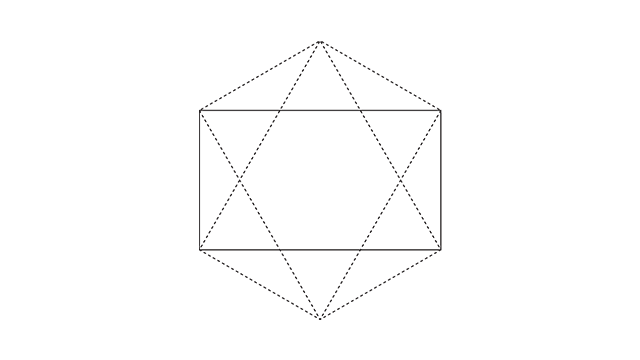
Para construir o hexágono você pode usar a ferramenta “polígono”, claro, mas como a ideia é te mostrar um pouco dos bastidores da construção geométrica, a gente vai pegar o retângulo raiz de 3, copiar com o “Ctrl+C”, colar na frente com o “Ctrl+F”, clicar na letra “R” do teclado para ativar a ferramenta “Rotate” e girar partindo desse vértice direito inferior até ele encostar no superior.

Caso seu Illustrator não esteja ligando estes vértices automaticamente você vai usar o atalho “Ctrl+U” para ativar as “Smart Guides”, ok?

Depois disso eu vou copiar e colar esse mesmo retângulo na frente dele de novo, apertar a letra “O” para ir para a ferramenta “Reflect”, e com o “Shift” pressionado, clicar e arrastar o mouse para a esquerda.

Pronto, você tem aí o hexágono perfeito.

Então para tirar a prova dos 9 eu vou desenhar o hexágono com a ferramenta “Polígono”, e enquanto eu desenho posso aumentar ou diminuir o número de lados apertando as teclas “seta para cima” ou “seta para baixo”.

Agora eu vou girar esse hexágono apertando “R” para habilitar a ferramenta “Rotate” novamente e dessa vez vou dar dois cliques nela para girar o meu objeto em 30 graus.

Só que você nota que a caixa de transformação dele acompanhou o giro, então para corrigir isso basta vir aqui em “Object/Transform/Reset Bounding Box”.

Pronto, agora eu vejo se ele bate certinho com o hexágono que eu construí “manualmente”.

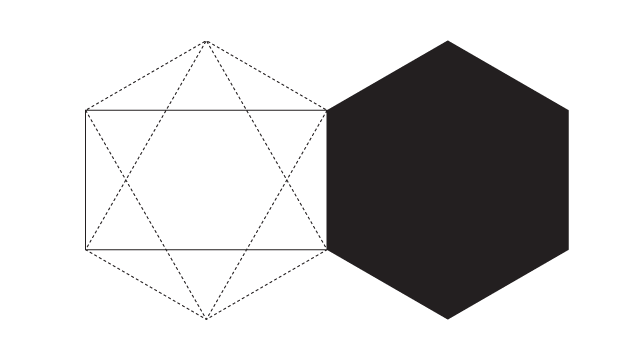
E tá aí, melhor que isso impossível.

A gente partiu do quadrado para construir o retângulo raiz de 2, que nos ajudou a construir o retângulo raiz de 3, e que finalmente nos ajudou a construir um hexágono.

E você não vai ficar surpreso se eu disser que existe um raiz de 4, raiz de 5, e por aí vai, né?

Retângulo áureo

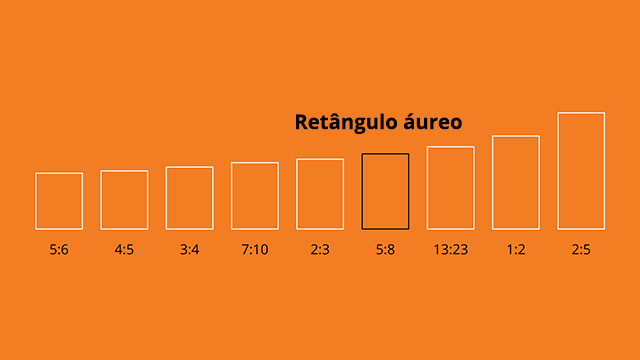
E agora vou te mostrar o último retângulo, que é talvez o mais famoso de todos, o retângulo áureo.

E assim como os anteriores, esse aqui também tem uma proporção entre os lados, e como a maioria aqui já deve saber, o resultado dessa proporção é 1,618.

E voltando aqui para o Illustrator, eu não preciso explicar muito o primeiro exemplo, já que o processo é exatamente o mesmo que você já viu até aqui, com a única diferença de que agora eu vou dividir o quadrado no centro vertical, copiar e colar esse quadrado na frente dele mesmo para te mostrar uma coisa daqui a pouco, agora sim puxo a linha diagonal, giro até encostar na base e aumento um dos quadrados até encostar no limite da linha.

E agora uma curiosidade, pessoal. Caso você ainda não saiba, esse retângulo menor que a gente encontrou é um retângulo áureo também.

Então só para garantir que eu não estou falando nenhuma bobagem, eu vou pegar a largura do meu retângulo maior, 242,705 e dividir pela altura, 150. O resultado é 1,618.

Agora eu pego o retângulo menor, que tem 150 de altura e divido por 92,705 de largura, e o resultado é 1,618.

O segundo método você também já viu. Vou na aba “Transform” e multiplico a largura por 1,618.

Pronto, você já aprendeu duas formas diferentes de construir o retângulo áureo usando o Illustrator.

E agora eu vou te mostrar uma terceira que talvez você não conheça, e dessa vez partindo do círculo, ao invés do quadrado.

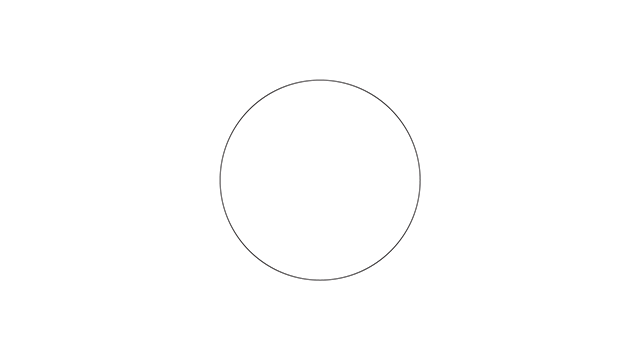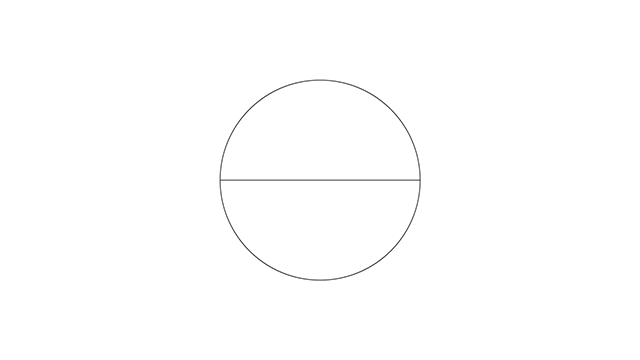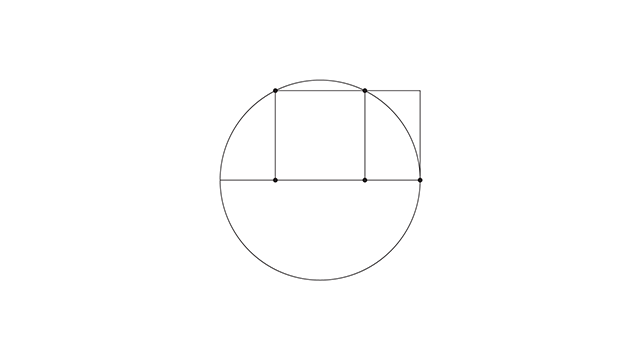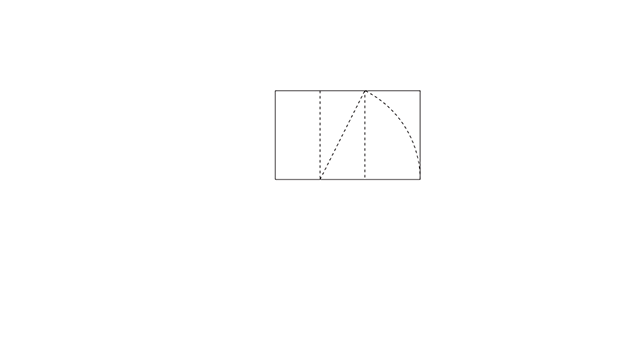
Você pega o círculo, divide ele no centro horizontal e desenha um quadrado partindo do centro até que as quinas encostem na borda do círculo.

Agora basta eu puxar um retângulo até a extremidade direita do círculo, e nós temos um novo retângulo áureo.

Na verdade há várias formas de encontrar o retângulo áureo mas eu vou deixar para você descobrir sozinho.

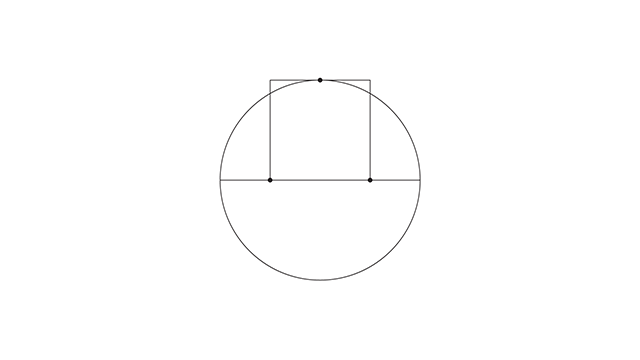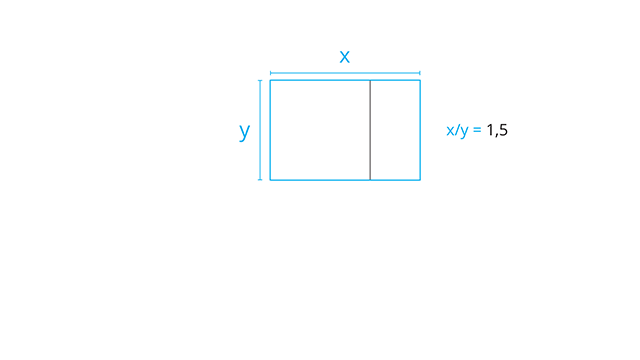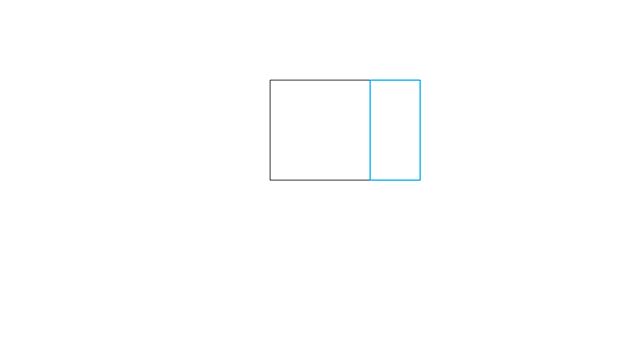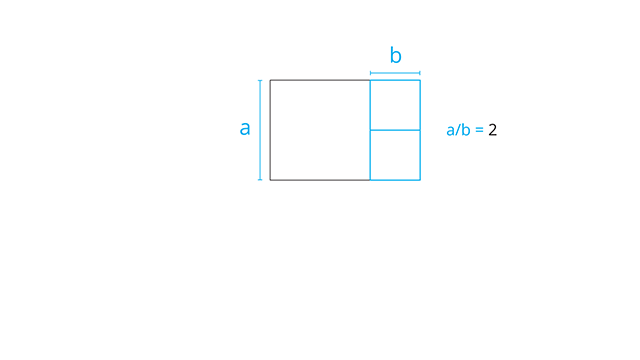
Deixa eu abrir um parêntese aqui rapidinho. Se você desenhar esse quadrado tangenciando o topo do círculo e puxar um retângulo a partir daí, esse retângulo maior tem proporção de 1,5, e o menor é exatamente um terço do maior.

Além disso, esse retângulo menor é dividido em dois quadrados exatamente iguais, o que faz desse retângulo o retângulo 1:2. Enfim, só a título de curiosidade mesmo.

E para finalizar sobre o retângulo áureo, uma curiosidade tirada do livro Geometria do Design, para variar.

No século 19 o filósofo e psicólogo Gustav Fechner fez um estudo de preferência entre diversos tipos de retângulos e descobriu que a maioria das pessoas preferia objetos com proporções iguais ou similares a do retângulo áureo.

A razão disso até hoje não foi muito bem explicada, mas apenas para citar um exemplo dessa preferência aqui na nossa época eu sugiro que você pegue seu cartão de visitas e divida a largura pela altura.

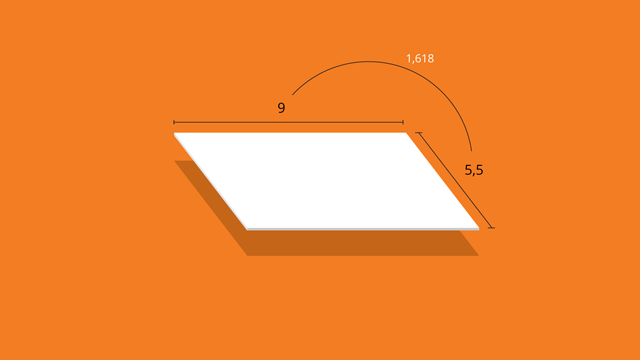
Eu garanto para você que o resultado vai ser bem próximo do retângulo áureo, principalmente se ele for um cartão de 9 x 5,5. Divide 9 por 1,618 para ver o valor você encontra.

Reparou que quanto mais você se aprofunda mais coisa interessante descobre?

Então quando alguém me pergunta como é possível que eu tenha adivinhado que o cartaz do Jan Tshichold foi dividido em círculos subdividos em 5 partes, ou que o símbolo do Chrome foi construído com base em um grid, guias e triângulos, na verdade eu não estou adivinhando nada, estou apenas sugerindo um dos caminhos possíveis com base no conhecimento que eu tenho. É uma suposição, não uma adivinhação. E esse conhecimento nada mais é do que treino e muito estudo e análise.

Esse processo de raciocínio é exatamente o mesmo que eu uso para construir minhas marcas. Não tem nada de diferente, especial, ou mesmo de extrema dificuldade, como as pessoas costumam achar.

Então, o fato de eu saber desenhar um pentágono no Illustrator é bom, claro, mas é melhor ainda se eu souber pelo menos uma forma de como construir esse pentágono, seja utilizando um compasso ou mesmo o próprio Illustrator. Isso só amplia as possibilidades que eu tenho de criar e de analisar designs diferentes.

E é exatamente isso que eu vou te mostrar agora. Vamos construir o pentágono. Ou você pensou que eu ia terminar esse vídeo sem ele?

Pentágono

O pentágono é um pouco mais complicado que os outros mas não deixa de ser simples.

A gente começa pelo círculo e encontra os centros vertical e horizontal utilizando a ferramenta linha.

Depois eu duplico essa linha vertical com o “Shift” e “Alt” pressionados até ela encostar na extremidade esquerda do círculo, e duplico ela mais uma vez para a direita pois eu preciso encontrar o centro entre essas duas verticais. Para isso eu seleciono as 3 linhas ao mesmo tempo e distribuo horizontalmente.

Crio um novo círculo mantendo o “Shift” e o “Alt” pressionados partindo desse ponto central até ele encostar nas duas guias externas.

Agora eu vou na ferramenta “linha” novamente e crio uma guia da base central do círculo grande até o centro do círculo menor.

Seleciono essa linha e aumento com o “Shift” pressionado até ela cruzar a extremidade do círculo menor.

Agora eu seleciono a seta preta e dou dois cliques nessa linha para entrar no modo de isolamento, aperto “Ctrl+Y” para enxergar somente outline, dou um zoom, aperto “+” no teclado para habilitar a ferramenta de adicionar pontos e crio um ponto na interseção entre essa linha e o círculo pequeno.

Agora eu excluo essa parte que sobrou com e já posso sair do modo de isolamento dando dois cliques fora com a seta preta.

Aperto “Ctrl+O” para centralizar a página e seleciono essa linha que a gente acabou de criar.

Apenas para você entender, eu deletei aquela ponta porque essa linha agora tem o mesmo tamanho do raio do círculo que eu preciso criar para continuar.

Então para criar um círculo com esse raio eu preciso da altura exata dessa linha. Para isso eu seleciono a ferramenta “Rotate” com o atalho “R”, clico na base da linha para marca a âncora e giro até a linha encostar na minha guia central e vertical.

Agora eu vou copiar a altura dessa linha, selecionar a ferramenta “Elipse”, clico em qualquer lugar da tela e colo esse valor que eu acabei de copiar no primeiro campo.

Depois que eu colar, eu multiplico esse valor por 2 e aperto a tecla “Tab” para aplicar a multiplicação. Eu multipliquei por dois porque como eu falei essa linha que a gente criou nos dá o raio, mas o Illustrator cria o círculo com base no diâmetro. Então como o raio é metade do diâmetro é só multiplicar o valor por dois.

Agora é só copiar o valor desse campo, colar no campo de baixo e clicar “Ok”.

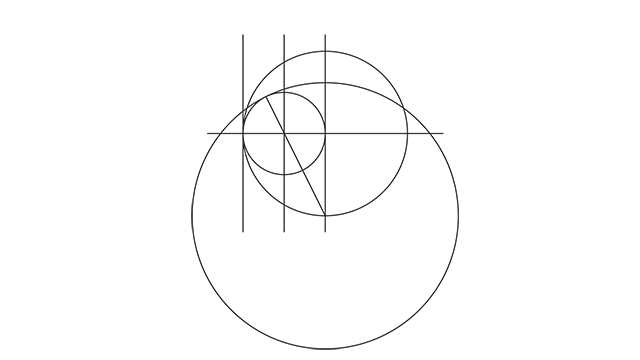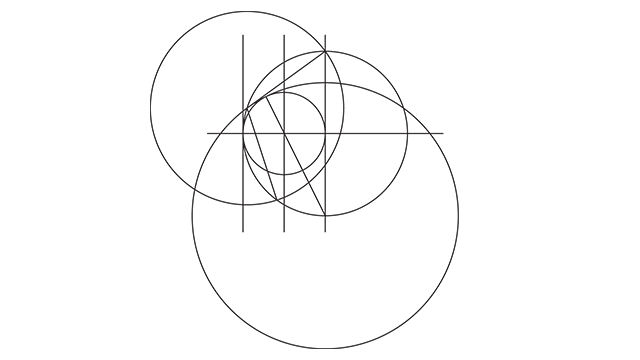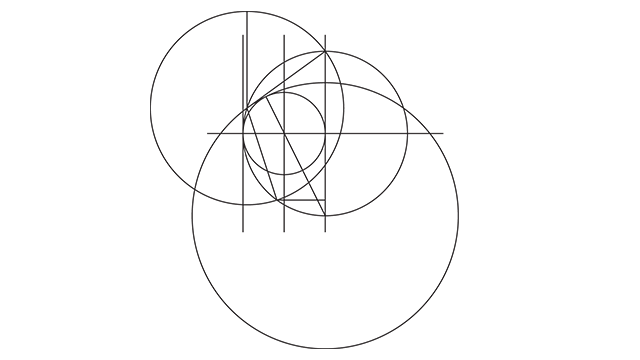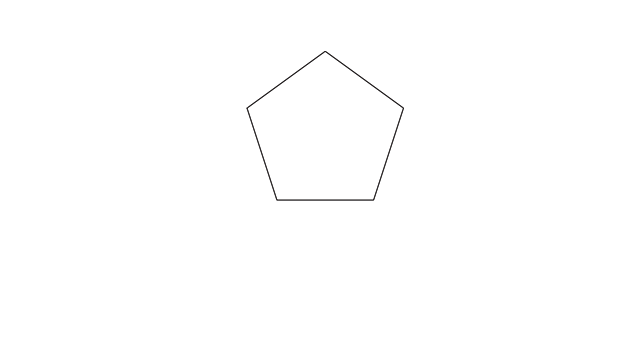
Alinho o centro desse círculo com a base do primeiro círculo criado e pronto, eles se tocam no ponto exato que a gente previu, e a gente acabou de encontrar esse ponto aqui, que é a interseção entre o primeiro círculo e esse último que a gente acabou de criar.

Agora eu preciso de um novo círculo que vá desse ponto que a gente acabou de encontrar até encostar no topo central do primeiro círculo.

O procedimento é exatamente o mesmo que o anterior. Crio a guia, giro até ela ficar na vertical, encontro o tamanho, e repito exatamente o mesmo procedimento do círculo anterior.

Agora é só alinhar o centro dele com a nossa interseção.

E fechou, agora a gente já tem o que precisa para finalizar o pentágono nessas 3 interseções que a gente encontrou.

Vou apertar “P” para ir para a ferramenta “Path” e desenhar metade do pentágono clicando nestes 3 pontos.

Seleciono esse novo objeto, “Ctrl+C” e “Ctrl+F” para colar na frente dele mesmo, vou na aba “Transform”, marco qualquer eixo direito referência e dou um “Flip Horizontal”.

Seleciono agora os dois objetos com o “Shift” pressionado, agrupo com o “Gtrl+G” e entro no modo de isolamento dando dois cliques. A ideia de entrar no modo de isolamento aqui é que eu posso fechar os pontos sem interferir nos outros objetos que estão fora dele.

Então eu uno esses aqui da ponta com o atalho “Ctrl+J” e faço a mesma coisa na base com os dois pontos abertos.

Posso sair do modo de isolamento e pronto, temos o nosso pentágono.

E só para provar que ele está correto eu posso criar um pentágono com a ferramenta “polígono”, sobrepor os dois e vejo que o pentágono está perfeito.

E agora eu vou te dar algumas curiosidades sobre o pentágono que a gente acabou de construir.

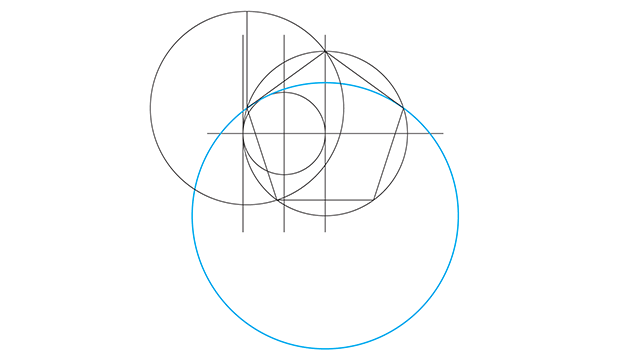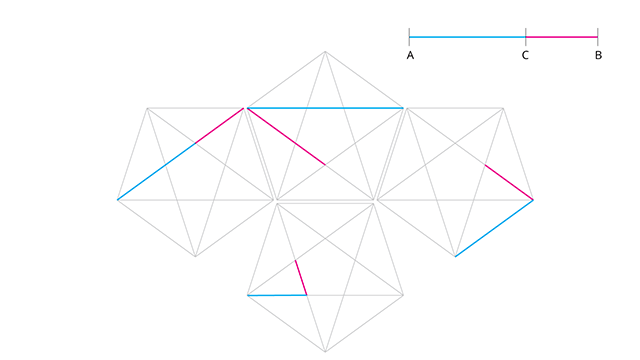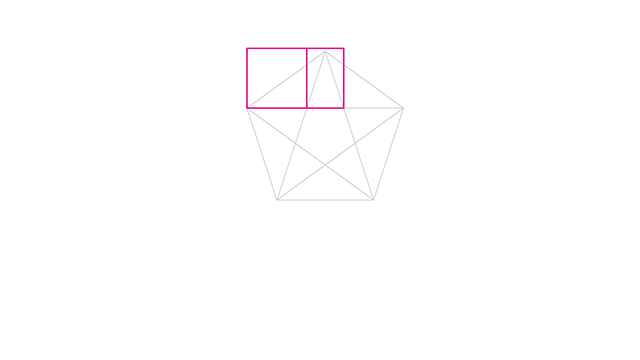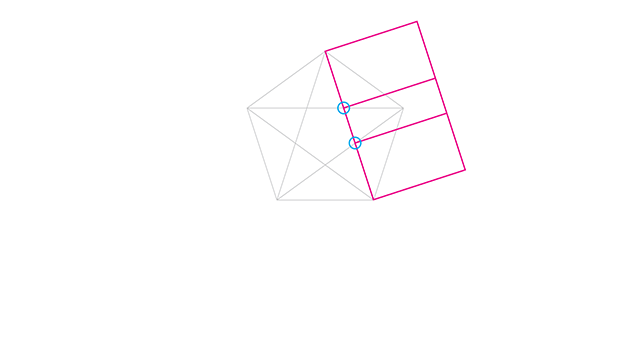
Se eu dividir o tamanho desse círculo maior que a gente utilizou na construção por 1,618 o resultado será um círculo exatamente do mesmo tamanho do primeiro círculo.

Se eu montar a estrela dentro do pentágono e dividir o tamanho da linha azul pelo tamanho da linha rosa em cada um desses exemplos, o resultado é 1,618.

Se eu criar um quadrado da ponta esquerda da estrela até a base da ponta superior, depois puxar um retângulo do mesmo ponto até a outra base da ponta superior eu tenho um retângulo áureo.

E por último, se eu inserir um retângulo áureo de uma ponta a outra da estrela eu também encontro interseções bem claras entre os dois objetos.

Ou seja, não basta dominar a sua ferramenta de trabalho, e eu espero que esse vídeo tenha contribuído em pelo menos despertar algumas curiosidades em você.

Eu posso ficar até amanhã falando sobre esse assunto mas a verdade é que eu já demorei duas semanas para montar esse vídeo, que deu bastante trabalho mas foi bem legal de fazer.

E eu vou encerrar agradecendo um leitor, que há algumas semanas me surpreendeu com um e-mail muito legal. Ele havia conseguido terminar o layout abaixo graças a um vídeo aqui do canal, que fez ele se inspirar e tentar utilizar um retângulo áureo para organizar esse projeto que estava parado havia algum tempo por falta de criatividade.

Layout por Mundo Studio

O mais curioso é que em momento algum eu dei sequer um exemplo parecido com esse que ele enviou. Ou seja, ele precisou de muito pouco para se inspirar e viajar na criação dele. O que significa que provavelmente ele já vinha estudando e buscando outras referências, acredito eu.

E o mais legal é ele ter falado que o projeto estava parado por falta de criatividade, e foi justamente um processo de construção que trouxe mais liberdade criativa para ele.

A verdade é que quanto mais você estuda e se inspira em métodos utilizados por outras pessoas, mais você pensa como as pessoas que utilizam estes métodos. Não tem mistério.

Então deixo aqui meu muito obrigado ao Ricardo, e aos outros leitores do blog e inscritos aqui do canal também.

Muito obrigado pelo suporte que vocês vêm dando para o conteúdo. E eu estou muito feliz por essa oportunidade de compartilhar e mais ainda pela troca que eu estou recebendo de vocês.

E caso você ainda não conheça o canal fique à vontade para ver os outros vídeos e se inscrever caso ache o conteúdo relevante para você.

Você também pode visitar meu blog, waltermattos.com, onde eu compartilho dicas, reflexões e tutoriais relacionados a design.

É isso aí pessoal. Um abraço e até o próximo vídeo.

--